La raison pour laquelle un sex-ratio inégal affecte la taille effective de la population est que la progéniture est produite par un parent mâle et une femelle, et un sex-ratio inégal augmente la vitesse à laquelle la dérive génétique se produira.
"... le plus petit nombre de mâles contribue encore à la moitié des gènes de la génération suivante ..."
En d'autres termes, en supposant que la population masculine est plus petite, les gènes transmis par les hommes / pères sont prélevés sur une population plus petite que celle des femmes / mères. Comme vous le savez, les petites populations sont plus sujettes à la dérive.
Imaginez l'exemple de dérive classique avec un sac de billes bleues et rouges, mais ayez la génération parentale avec un nombre inégal de billes dans les deux sacs.
Hartl & Clark illustre (voir figure 4 ici) la relation entre le sex-ratio et la taille effective de la population, où un sex-ratio de 1: 9 donne une taille effective de population d'environ 36% de la taille réelle (étant donné de 100 $ \ fois (N_e / N) $). Cela signifie que le taux de consanguinité et de dérive dans la population focale est équivalent à celui d'une population idéalisée qui est 0,36 fois la taille du recensement de la population focale.
$$ N_e = \ frac {4N_mN_f} {N_m + N_f} = \ frac {4 \ fois 1 \ fois 9} {1 + 9} = 3,6 $$
La population est diploïde et dioïque ; chaque parent porte deux gènes, et chaque parent doit être remplacé au sein de la population afin que chaque paire doit produire deux descendants. Prenons le cas où $ N_m = N_f = 1 $ (et donc $ N = N_e = 2 $). Le nombre de gènes dans cette population est de quatre. Par conséquent, pour maintenir la même taille de population, quatre gènes doivent être tirés de la population ancestrale.
Lectures complémentaires:
Bien que (personnellement) je ne puisse pas le prouver mathématiquement, je peux le démontrer en utilisant la simulation. J'ai rédigé un simulateur de dérive génétique dans R, qui peut faire face à des sex-ratios inégaux.
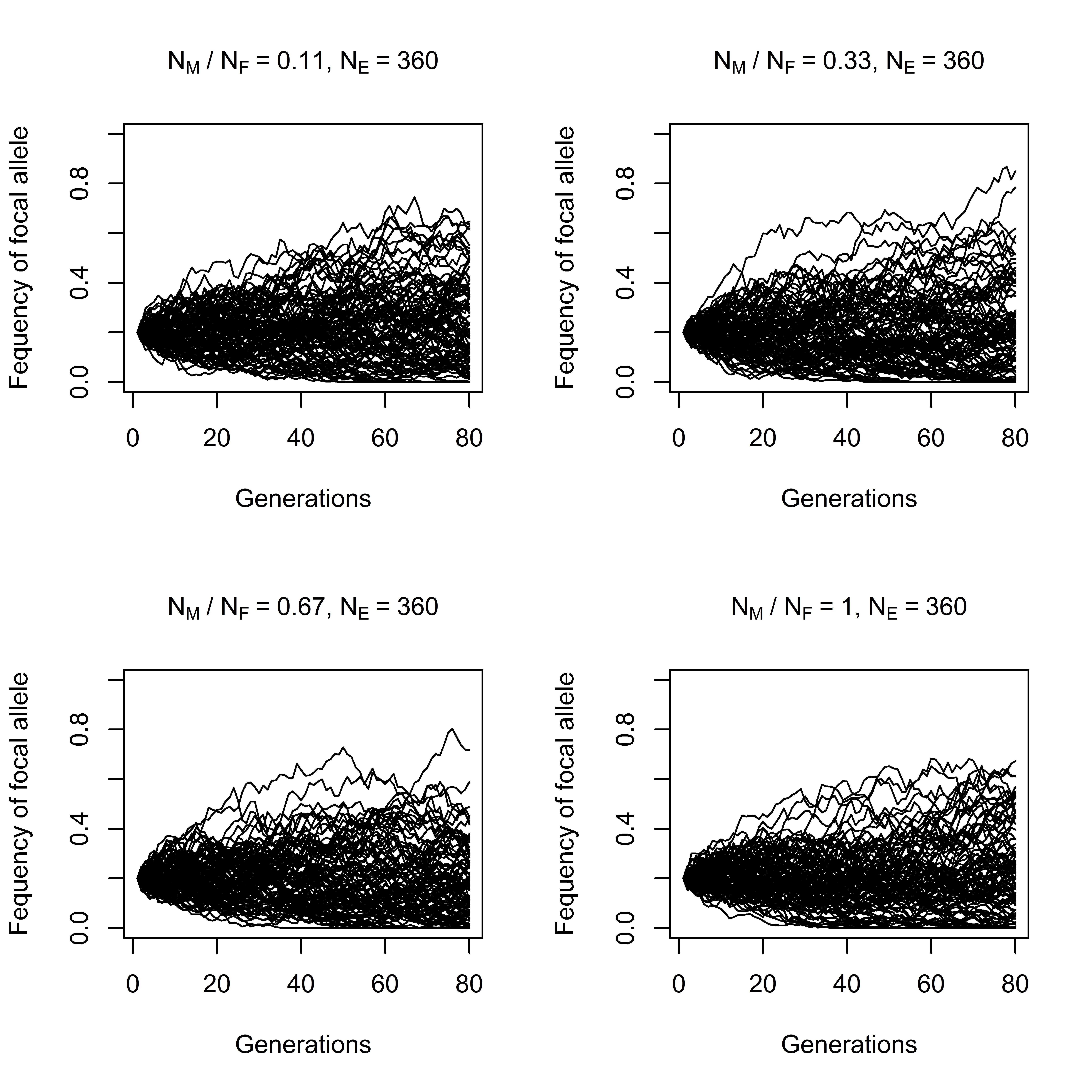
Les quatre premiers graphiques sont des populations avec $ N_E = 360 $ à différents rapports de masculinité ($ N_M / N_F $ = 0,11, 0,33, 0,67, 1,00), pour 100 populations répliquées simulées sur 80 générations, avec une fréquence allélique initiale de 0,2. Les quatre simulations ont une taille de population de recensement différente, mais une taille de population effective égale, en raison du sex-ratio. Les quatre groupes de populations se comportent de la même manière (les taux de dérive sont similaires pour les populations simulées dans les différentes conditions).
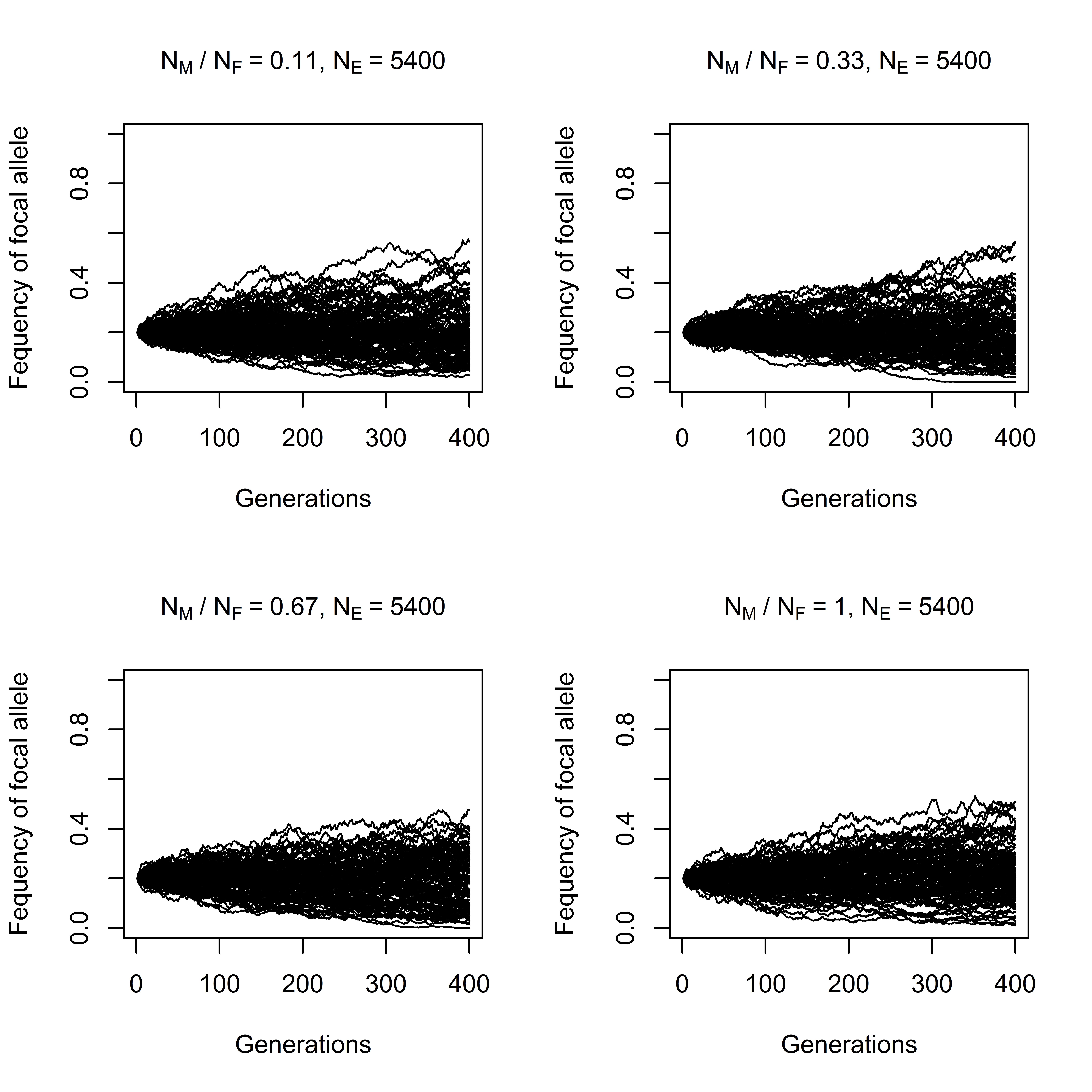
Ces quatre utilisent des populations plus importantes ($ N \ fois 15 $), aux mêmes rapports sexuels, où $ N_E = 5400 $ dans tous les cas simulés sur 400 générations. Encore une fois, les groupes de simulations se comportent de la même manière.
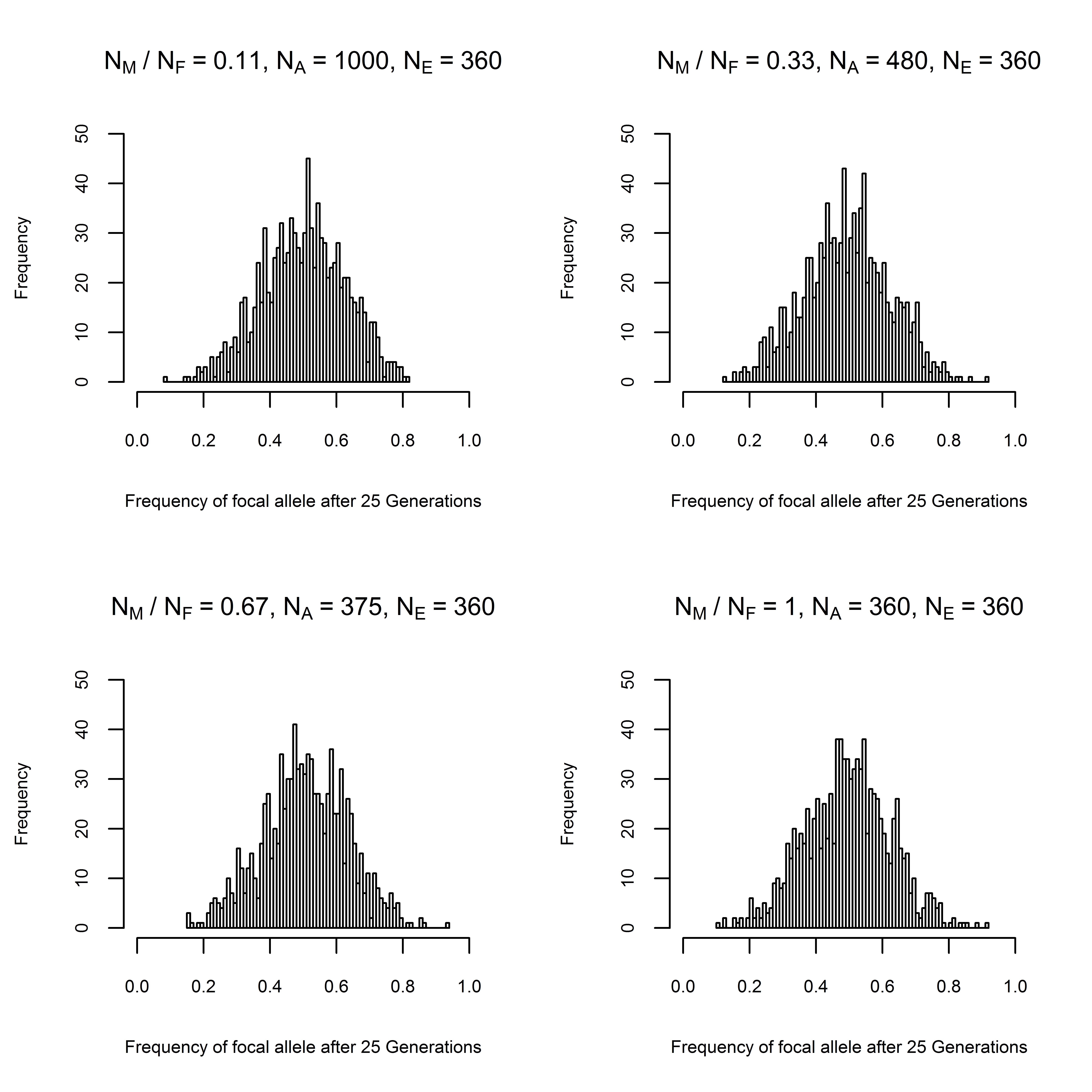
J'ai ajouté des histogrammes pour faciliter la visualisation du modèle, en utilisant $ P = 0,5 $, pour 1000 populations simulées sur 25 générations, où $ N_E = 360 $ et le rapport taille / sexe de la population du recensement varie entre les simulations. Ces distributions sont similaires malgré les différentes tailles de population du recensement.